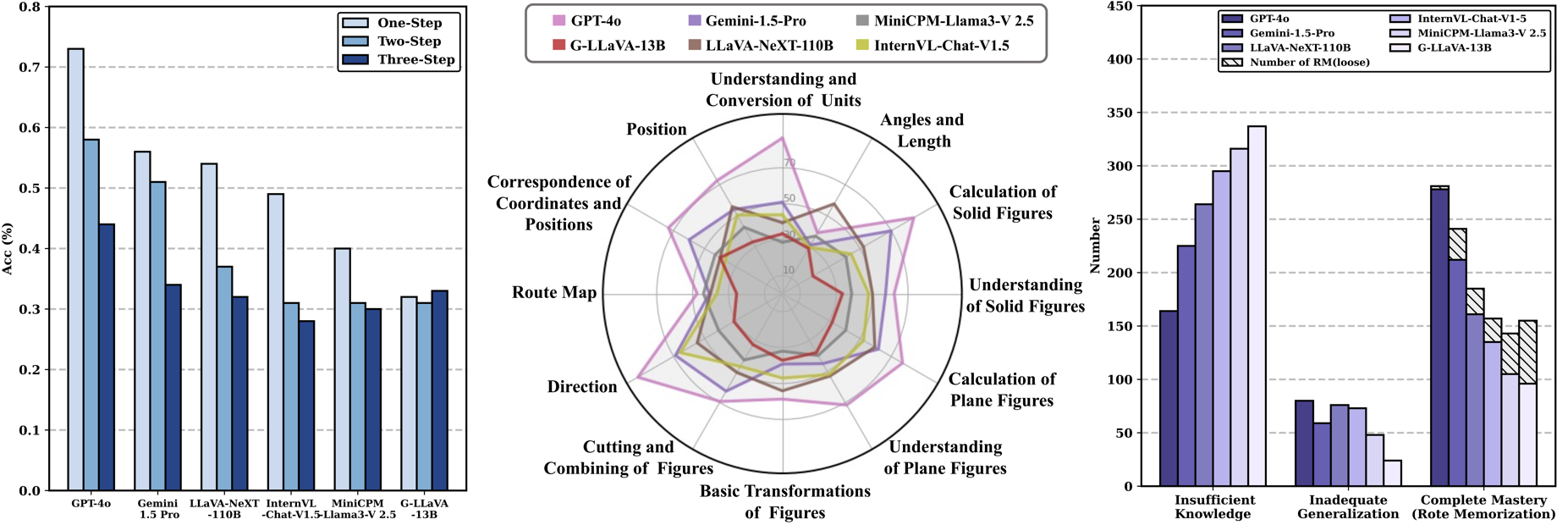
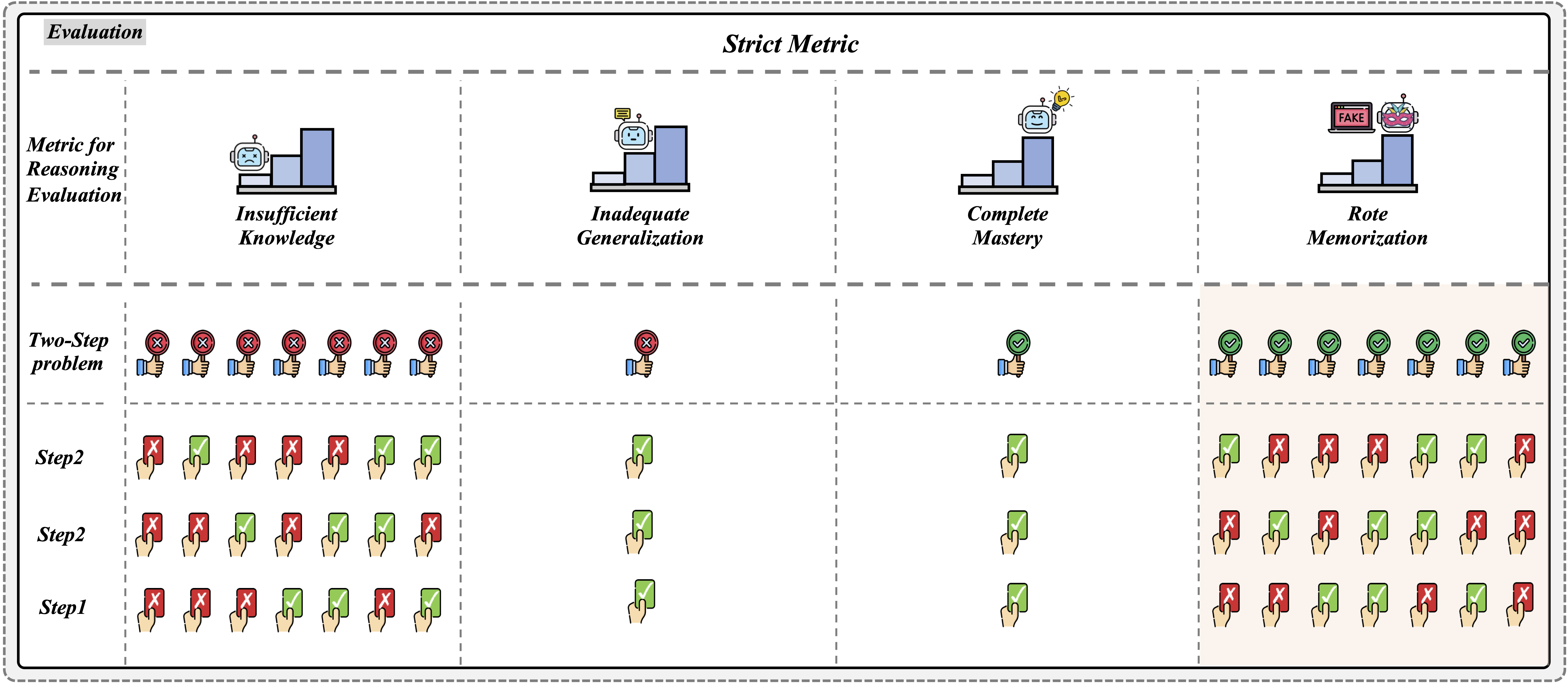
Accuracy scores on the testmini subset (1,740 examples) of ![]() We-Math.
We-Math.
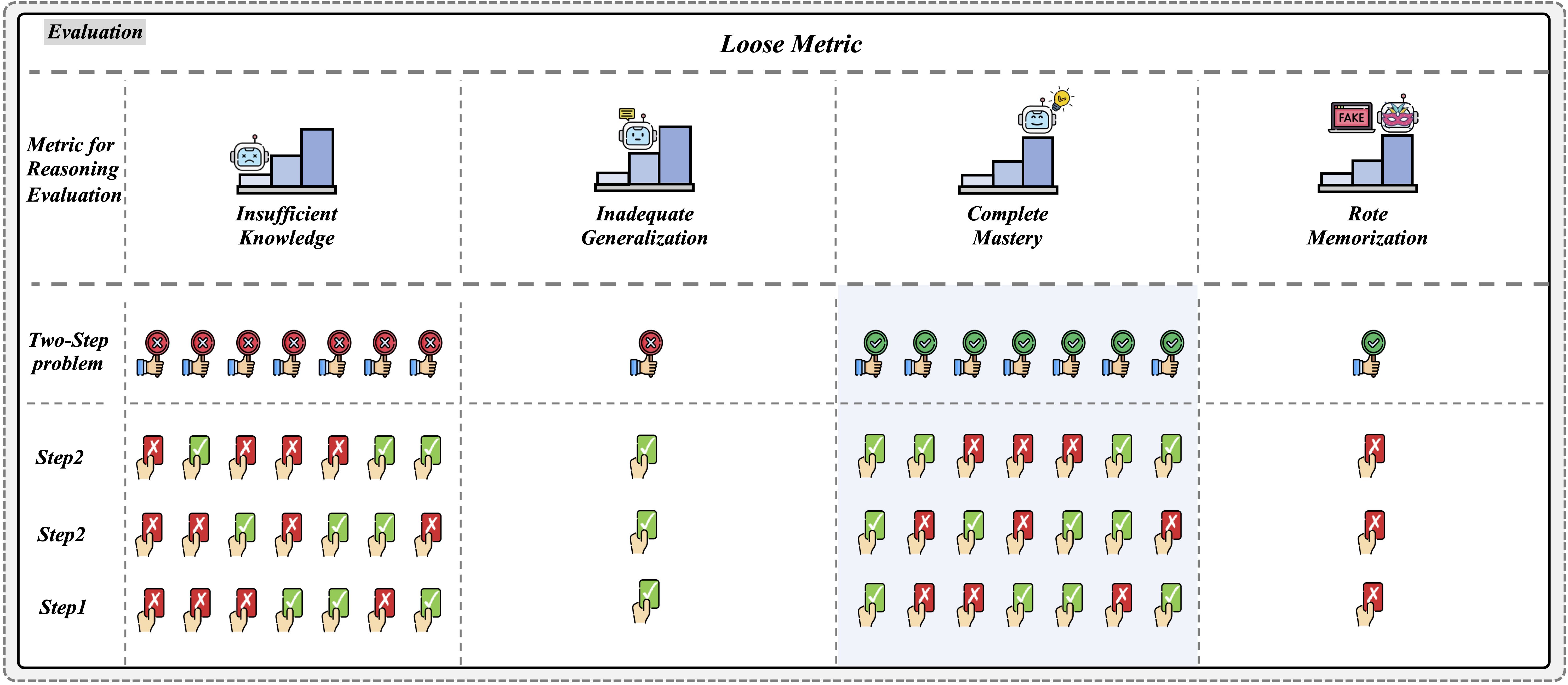
More results can be found on the OpenCompass! We recommend using VLMEvalKit for evaluation, and adopting the Strict Score as the reported metric.
| # | Model | Source | Date | Avg(Strict) | IK(Strict) | IG(Strict) | CM(Strict) | RM(Strict) | Avg(Loose)
| IK(Loose) |
IG(Loose) |
CM(Loose) |
RM(Loose) |
|
| 1 | Gemini-2.5-Pro 🥇 | Link | - | 78.0% | - | - | - | - | - | - | - | - | - |
| 2 | Seed1.5-VL | Link | - | 77.5% | - | - | - | - | - | - | - | - | - |
| 3 | Doubao-1.5-Pro | Link | - | 65.7% | - | - | - | - | - | - | - | - | - |
| 4 | GPT-4.1-20250414 | Link | - | 55.5% | - | - | - | - | - | - | - | - | - |
| 5 | GPT-4o | Link | - | 50.6% | - | - | - | - | - | - | - | - | - |
| 6 | Qwen2.5-VL-72B | Link | - | 49.1% | - | - | - | - | - | - | - | - | - |
| 7 | InternVL3-78B | Link | - | 46.1% | - | - | - | - | - | - | - | - | - |
| 8 | InternVL3-8B | Link | - | 39.5% | - | - | - | - | - | - | - | - | - |
| 9 | URSA-8B-PS-GRPO | Link | - | 38.3% | - | - | - | - | - | - | - | - | - |
| 10 | InternVL2-Llama3-76B | Link | 2024-07 | 36.86% | 33.90% (178) | 15.81% (83) | 28.95% (152) | 42.42% (112) | 56.29% | 33.90% (178) | 15.81% (83) | 48.38% (254) | 3.79% (10) |
| 11 | Qwen2-VL-72B | Link | 2024-05 | 36.57% | 33.52% (176) | 14.10% (74) | 29.52% (115) | 43.64% (120) | 56.76% | 33.52% (176) | 14.10% (74) | 49.71% (261) | 5.09% (14) |
| 12 | Qwen2.5-VL-7B | Link | - | 36.2% | - | - | - | - | - | - | - | - | - |
| 13 | MM-Eureka-7B | Link | - | 34.7% | - | - | - | - | - | - | - | - | - |
| 14 | URSA-8B | Link | - | 32.8% | - | - | - | - | - | - | - | - | - |
| 15 | GPT-4V | Link | 2024-04 | 31.05% | 39.81% (209) | 14.48% (76) | 23.81% (125) | 47.92% (115) | 51.43% | 39.81% (209) | 14.48% (76) | 44.19% (232) | 3.33% (8) |
| 16 | R1-Onevision-7B | Link | - | 30.0% | - | - | - | - | - | - | - | - | - |
| 17 | InternVL2.5-8B | Link | - | 23.5% | - | - | - | - | - | - | - | - | - |
| 18 | Gemini 1.5 Pro | Link | 2024-05 | 26.38% | 42.86% (225) | 11.24% (59) | 20.76% (109) | 54.77% (132) | 46.00% | 42.86% (225) | 11.24% (59) | 40.38% (212) | 12.03% (29) |
| 19 | Qwen-VL-Max | Link | 2024-01 | 10.48% | 65.14% (342) | 7.62% (40) | 6.67% (35) | 75.52% (108) | 25.52% | 65.14% (342) | 7.62% (40) | 21.71% (114) | 20.28% (29) |
| 20 | LLaVA-OneVision-72B | Link | 2024-05 | 28.67% | 41.14% (216) | 16.19% (85) | 20.57% (108) | 51.79% (116) | 49.05% | 41.14% (216) | 16.19% (85) | 40.95% (215) | 4.02% (9) |
| 21 | InternVL-Chat-V1.5 | Link | 2024-04 | 14.95% | 56.19% (295) | 13.90% (73) | 8.00% (42) | 73.25% (115) | 32.67% | 56.19% (295) | 13.90% (73) | 25.71% (135) | 14.01% (22) |
| 22 | LLaVA-1.6-13B | Link | 2024-03 | 5.24% | 69.14% (363) | 3.24% (17) | 3.62% (19) | 86.90% (126) | 22.00% | 69.14% (363) | 3.24% (17) | 20.38% (107) | 26.21% (38) |
| 23 | G-LLaVA-13B | Link | 2024-03 | 6.48% | 64.19% (337) | 4.57% (24) | 4.19% (22) | 86.59% (142) | 22.29% | 64.19% (337) | 4.57% (24) | 20.00% (105) | 35.98% (59) |
| 24 | GLM-4V-9B | Link | 2024-06 | 14.86% | 52.95% (278) | 9.52% (50) | 10.10% (53) | 73.10% (144) | 35.05% | 52.95% (278) | 9.52% (50) | 30.29% (159) | 19.29% (38) |
| 25 | InternVL2-8B | Link | 2024-07 | 26.57% | 45.52% (239) | 13.52% (71) | 19.81% (104) | 51.63% (111) | 44.86% | 45.52% (239) | 13.52% (71) | 38.10% (200) | 6.98% (15) |
| 26 | Qwen2-VL-7B | Link | 2024-09 | 25.62% | 47.05% (247) | 14.67% (77) | 18.29% (96) | 52.24% (105) | 42.95% | 47.05% (247) | 14.67% (77) | 35.62% (187) | 6.97% (14) |
| 27 | LLaVA-OneVision-7B | Link | 2024-08 | 23.14% | 44.95% (236) | 13.14% (69) | 16.57% (87) | 60.45% (133) | 44.86% | 44.95% (236) | 13.14% (69) | 38.29% (201) | 8.64% (19) |
| 28 | MiniCPM-LLaMA3-V 2.5 | Link | 2024-05 | 9.52% | 60.19% (316) | 9.14% (48) | 4.95% (26) | 83.85% (135) | 28.00% | 60.19% (316) | 9.14% (48) | 23.43% (123) | 23.60% (38) |
| 29 | LongVA-7B | Link | 2024-06 | 11.52% | 61.14% (321) | 8.95% (47) | 7.05% (37) | 76.43% (120) | 27.71% | 61.14% (321) | 8.95% (47) | 23.24% (122) | 22.29% (35) |
| 30 | InternLM-XComposer2-VL-7B | Link | 2024-04 | 12.67% | 56.38% (296) | 10.48% (55) | 7.43% (39) | 77.59% (135) | 30.95% | 56.38% (296) | 10.48% (55) | 25.71% (135) | 22.41% (39) |
| 31 | LLaVA-1.6-7B | Link | 2024-03 | 3.33% | 78.29% (411) | 2.48% (13) | 2.10% (11) | 89.11% (90) | 13.81% | 78.29% (411) | 2.48% (13) | 12.57% (66) | 34.65% (35) |
| 32 | Phi3-Vision-4.2B | Link | 2024-05 | 10.57% | 58.86% (309) | 8.95% (47) | 6.10% (32) | 81.07% (137) | 29.81% | 58.86% (309) | 8.95% (47) | 25.33% (133) | 21.30% (36) |
| 33 | DeepSeek-VL-1.3B | Link | 2024-03 | 5.90% | 71.05% (373) | 2.67% (14) | 4.57% (24) | 82.61% (114) | 21.52% | 71.05% (373) | 2.67% (14) | 20.19% (106) | 23.19% (32) |
🚨 To submit your results to the leaderboard, please send to this email with your result json files.